Materi Kelas VII tgl 27 mei 2020

-
HUBUNGAN DUA SUDUT DAN ANTAR SUDUT

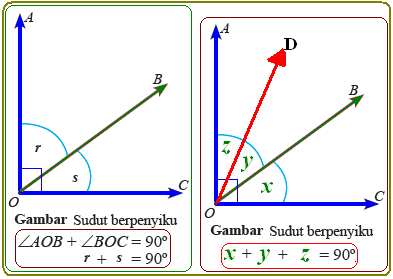
 A. SUDUT YANG SALING BERPENYIKU
Dikatakan saling berpenyiku, jika jumlah kedua sudut nya 90 derajat

     
B. SUDUT SALING BERPELURUS
Dikatakan saling berpelurus, jika jumlah kedua sudut nya 180 derajat.


C. SUDUT  SALING SEHADAP

 D. SUDUT DALAM BERSEBRANGAN

 E. SUDUT LUAR BERSEBRANG

F.SUDUT DALAM SEPIHAK

 G. SUDUT LUAR SEPIHAK

 H. SUDUT SALING BERTOLAK BELAKANG

Sudut Garis Sejajar

  1. Sudut sehadap, besarnya sama. Yakni ∠1 = ∠5, ∠2 = ∠6, ∠4 = ∠8, ∠3 = ∠7.
  2. Sudut dalam berseberangan, besarnya sama. Yakni ∠3 = ∠5, ∠4 = ∠6
  3. Sudut luar berseberangan, besarnya sama. Yakni ∠1 = ∠7, ∠2 = ∠8
  4. Sudut dalam sepihak, jumlah keduanya adalah 180°. Yakni ∠4 + ∠5 = 180°, ∠3 + ∠6 = 180°.
  5. Sudut luar sepihak, jumlah keduanya adalah 180°. Yakni ∠2 + ∠7 = 180°, ∠1 + ∠8 = 180°.
  6. Sudut bertolak belakang, besarnya sama. Yakni ∠1 = ∠3, ∠2 = ∠4, ∠5 = ∠7, ∠6 = ∠8.

OK SAMPAI DISINI MATERINYA YA!!!
CATAT DIBUKU CATATANMU 
!!


Sekarang Ayo Berlatih Contoh Soal-Soal.
PINDAHKAN CONTOH SOAL-SOAL BERIKUT DI BUKU LATIHANMU YA!!

1. Tentukanlah nilai a pada setiap gambar di bawah ini.
Soal 1
jawab: Sudut 2a dan 3a saling berpenyiku
⇔ 2a + 3a = 90°
⇔ 5a = 90°
⇔ a = 90° / 5
 Diperoleh nilai a = 18

 Ketiga sudut saling berpelurus
⇔ 46° + (a + 29°) + (5a + 15°) = 180°
⇔ 46° + 29° + 15° + 6a = 180°
⇔ 6a = 180° - 90°
⇔ 6a = 90°
⇔ a = 90° / 6
Diperoleh nilai a = 15
2. Perhatikan gambar!
soal9
Besar ∠BAC adalah ….
Perhatikan bahwa ACD adalah garis lurus. Sehingga ∠ACB dan ∠DCB saling berpelurus. Dengan demikian sehingga ∠ACB = 180 - 108 = 72. Selanjutnya, karena jumlah besar sudut-sudut segitiga adalah 180, maka diperoleh: ∠BAC+∠ACB+∠ABC = 180
∠BAC + 72 + 36 = 180
∠BAC = 180 -72- 36
∠BAC = 72.

 3. Perhatikan gambar
- Pada gambar a) 
Jika besar sudut x = 25°
                              y = 30°
maka, besar sudut Z =  25°

- Pada gambar b)
Jika besar sudut p = 45°
                              q = 40°
                               r = 35°
 maka besar sudut s  = 60°

4. Perhatikan gambar!





Besar sudut BAC adalah ….
Pembahasan:
Jumlah ketiga sudut pada segitiga sama dengan 180o:
  \[ 2x + 4^{o} + 8x + 1^{o} + 4x + 7^{o} = 180^{o} \]
  \[ 2x + 8x + 4x + 4^{o} + 1^{o} + 7^{o} = 180^{o} \]
  \[ 14x + 12^{o} = 180^{o} \]
  \[ 14x = 180^{o} - 12^{o} \]
  \[ 14x = 168^{o} \]
  \[ x = \frac{168^{o}}{14} = 12^{o}\]
Sehingga, besar sudut BAC adalah
  \[ \angle BAC = 2x + 4^{o} \]
  \[ = 2 \times 12^{o} + 4^{o} \]
  \[ = 24^{o} + 4^{o} \]
  \[ = 28^{o} \]

5. Perhatikan gambar berikut!





besar sudut pelurus

Besar pelurus sudut KLN adalah ….
A.       31o
B.       72o
C.       85o
D.       155o
Pembahasan:
Ingat, jumlah sudut yang berpelurus adalah 180o.
Sehingga,
  \[ (3x+15^){o} + (2X+10)^{o} = 180^{o} \]
  \[ 3x + 2x +15^{o} + 10^{o} = 180^{o} \]
  \[ 5x + 25^{o} = 180^{o} \]
  \[ 5x = 180^{o} - 25^{o} \]
  \[ 5x = 155^{o} \]
  \[ x = \frac{165^{o}}{5} = 31^{o} \]
Maka, besar pelurus sudut KLN = besar sudut MLN
  
6. Perhatikan gambar berikut!null





contoh variasi soal besar sudut

Besar \angle BAC adalah ….
A.       78o
B.       76o
C.       55o
D.       50o
Pembahasan:
Hitung besar \angle ACB!
  \[ \angle ACB + \angle BCD = 180^{o} \]
  \[ \angle ACB + 114^{o} = 180^{o} \]
  \[ \angle ACB = 180^{o} - 114^{o} = 66^{o} \]
Selanjutnya hitung nilai x melalui segitiga ACB. Perhatikan \Delta ABC
INGAT!!! Jumlah ketiga sudut pada segitiga adalah 180o.
  \[ \angle BAC + \angle ABC + \angle ACB = 180^{o} \]
  \[ x + x + 4^{o} + 66^{o} = 180^{o} \]
  \[ 2x + 70^{o} = 180^{o} \]
  \[ 2x = 180^{o} - 70^{o} \]
  \[ 2x = 110^{o} \]
  \[ x = \frac{110^{o}}{2} = 55^{o} \]
Besar \angle BAC = x = 55^{o}

Komentar

Posting Komentar

terimakasih atas komentar yang membangun

Postingan populer dari blog ini

GARIS DAN SUDUT SMP KLS 7 (PERTEMUAN KE-5)

-
Gambar
GARIS DAN SUDUT Garis A. Pengertian Garis Garis ialah titik titik tak terhingga yang disusun berderet dan bersebelahan kedua arah sehingga bentuknya memanjang, baik ke arah atas/bawah ataupun kiri/kanan.  B. Kedudukan dua buah garis Kedudukan dua buah garis  yaitu meliputi: Gambar Kedudukan Dua Garis Sudut A. Pengertian Sudut Pengertian sudut ialah dua buah garis sinar yang membentuk suatu daerah karena titik pangkalnya saling berhimpit atau bersekutu. Sudut tersebut memiliki bagian bagiannya sendiri. Berikut bagian bagian pada sudut yaitu meliputi: Kaki sudut ialah garis sinar yang digunakan untuk menciptakan sudut. Titik sudut ialah titik potong atau titik pangkal yang digunakan garis sinar untuk saling berhimpitan. Daerah sudut ialah ruang atau daerah yang terdapat di antara dua buah kaki sudutnya. Gambar Bagian Bagian Sudut B. Jenis-Jenis Sudut Sudut dapat dibagi menjadi beberapa macam yaitu meliputi: Gambar Jenis-Jenis Sudut
Baca selengkapnya

Pajak, Denda, dan Bonus (bagian 4)

-
Gambar
 PAJAK, DENDA DAN BONUS Pengertian Pajak, Denda dan Bonus Pajak adalah suatu kewajiban yang dibebankan kepada masyarakat untuk menyerahkan sebagian kekayaan kepada negara menurut peraturan-peraturan yang telah ditetapkan pemerintah. Jadi, pajak bersifat mengikat dan memaksa. Denda adalah    saksi berupa keharusan membayar segala bentuk sanksi administrasi karena yerlambat pajak, melanggar aturan, undang-undang dan lain Bonus adalah upah tambahan sebagai hadiah untuk menarik peminat atau sebagai penyemangat untuk mencapai prestasi yang lebih baik lagi. CONTOH SOAL   Pak  Putu memperoleh gaji Rp 1.000.000,00 sebulan dengan penghasilan tidak kena pajak Rp 400.000,00. Jika pajak penghasilan (PPh) diketahui 10%, berapakah besar gaji yang diterima Pak Putu per bulan? PENYELESAIAN: Besar gaji = Rp 1.000.000,00; Penghasilan tidak kena pajak = Rp 400.000,00 PPh = 10% Besar penghasilan kena pajak = Rp 1.000.000,00 – Rp 400.000,00 = Rp 600.000,00
Baca selengkapnya