Barisan dan Deret Geometri

Materi Matematika SMP Pencawan 

Rabu,26 Agustus 2020

Petunjuk:

1. Catat Materi ke buku catatan Matematika mu

2. Pelajari dan Pahami

3. Jika sudah selesai, kirim poto ke grup khusus          Matematika

4. Selamat belajar!!

Barisan Dan Deret Geometri : Materi SMP Kelas 8 

     Baris Geometri adalah barisan yang mempunyai perbandingan (rasio)tetap pada setiap dua suku yang berurutan. Ciri-cirinya  perkalian atau pembagian.

    Perbedaan dengan barisan aritmatika yaitu barisan aritmatika memiliki pertambahan dan pengurangan yang tetap, sedangkan barisan geometri memiliki perbandingan tetap berupa perkalian atau pembagian

Rumus Baris Geometri

    Untuk mencari suku ke-n (U-n)digunakan rumus:

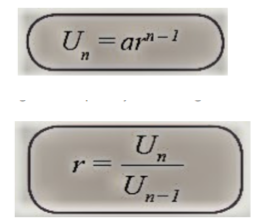
Un     = Suku ke n

Un-1 = Suku ke n –1

r       = Rasio

a      = Suku pertama

Contoh Baris Geometri

3, 6, 12, 24, 48, 96, … dan seterusnya

1, 3, 9, 27, 81, 243, … dan seterusnya

2, 6, 18, 54, 162, 486, … dan seterusnya

Jika Anda memperhatikan contoh baris geometri diatas, perbandingan dari barisan yang berurutan tetap.

6/3 = 12 /6 = 24/12  = 48/24    = 96/48    = 2

3 /1 =  9 /3  = 27/9  = 81/27    =  243 /81 = 3

6 /2 = 18/6  = 54 /18 = 162/54 = 486 /162 = 3

Contoh Soal Dan Pembahasan Baris Geometri

Soal 1: Tentukan suku ke 11  dari barisan geometri 3, 9, 27, 81, …

Jawab :

a      = 3

r      = Un / Un-1       = 9 / 3
       = 3

Un     = arn-1U11   = 3 . 3 11- 1        = 3 . 3 10        = 3. 59049
= 177.147

Jadi suku ke 11 dari barisan geometri tersebut yaitu 177.147

Soal 2: Diketahui barisan geometri 1, 4, 16, 64, … Tentukan suku ke 7 dari barisan geometri tersebut

Jawab :

a      = 1

r      = Un / Un-1        = 4 / 1
        = 4

Un     = arn-1U11   = 1 . 4 7- 1        = 1 . 4 6        = 1 . 4096
        = 4.096

Jadi suku ke 7 dari barisan geometri tersebut yaitu 4.096

Soal 3: Tentukan rasio dan suku ke 6 dari barisan deret geometri 2, 8, 32, 148, …

Jawab :

r      = Un/ Un-1        = 8 / 2
        = 4

U6     = 2 . 4 6- 1         = 2 . 4 5         = 2. 1204
= 2.048

Jadi rasio dari barisan geometri adalah 4 dan suku keenam adalah 2.048.

Deret Geometri

Deret Geometri sama halnya dengan deret aritmatika, perbedaannya yaitu deret geometri dengan perbandingan perkalian atau pembagian, sedangkan aritmatika dengan pertambahan atau pengurangan.

Deret Geometri Adalah jumlah suku dari barisan geometri yang mempunyai perbandingan atau rasio yang tetap.

Contoh Deret Geometri

1)  3, 6, 12, 24, 48, 96, …, Un

      Maka deret Geometri yaitu :

      3  + 6 + 12 + 48 + 96 + …+ Un

2)  1, 5, 25, 125, 625, …, Un

      Maka deret Geometri yaitu :

      1  + 5 + 25 + 125 + 625 + …+ Un

 

Rumus Deret Geometri

Rumus jumlah suku ke-n (Sn) adalah:

rumus deret geometri

Sn          = Jumlah suku ke n

r           = Rasio

a          = Suku pertama

Contoh Soal Dan Pembahasan Deret Geometri

Soal 1: Diketahui barisan geometri memiliki suku pertama atau a yaitu 8 dan rasio 2. Tuliskan barisan dan deret geometri

Jawab   :

Barisan Geometri yaitu 8, 16, 32, 64, 128, 256, …, Un

Deret Geometri yaitu  8 + 16 + 3 + 64 + 128 + 256 + … + Un

Soal2: Tentukan jumlah 7 suku pertama dari barisan 2, 4, 6, 8, …

Jawab   :

a      = 2

r      = Un / Un-1
       = 4 / 2
= 2

Sn      = a ( rn – 1 ) / ( r – 1 )

S7    = 2 ( 27 – 1 ) / (2 – 1)
= 2 ( 128- 1 ) / 1
= 2 . 127
= 254