JARAK DUA TITIK SMA kls XII

- September 22, 2020

JARAK DUA TITIK

A. Jarak dua titik jika diketahui titik kordinanya.

Diketahui dua titik A dan B dengan koordinat berturut-turut adalah $A(x_{1}, y_{1}, z_{1})$ dan $A(x_{2}, y_{2}, z_{2})$ . Jarak titik A dan B dapat dicari menggunakan rumus berikut.

$\left| AB \right| = \sqrt{(x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2} + (z_{1} - z_{2})^{2}}$

Contoh soal dan pembahasan jarak titik ke titik jika diketahui koordinat letaknya.

Tentukan jarak antara dua titik yang memiliki koordinat P(0, 7, 6) dan Q(5, 2, 1)!

Pembahasan:

$\left| PQ \right| = \sqrt{0 - 5)^{2} + (7 - 2)^{2} + (6 - 1)^{2}}$

$=\sqrt{(-5)^{2} + (5)^{2} + 5^{2}}$

$=\sqrt{25+ 25 + 25}$

$=\sqrt{75}$

$=\sqrt{25 \cdot 3}$

$=\sqrt{25} \cdot \sqrt{3}$

$=5\sqrt{3}$

B. Jarak dua titik pada bangun ruang

Selain contoh soal di atas, akan diberi contoh soal cara menentukan jarak antara dua titik pada bangun ruang. Simak contoh soalnya di bawah!

Contoh Soal dan Pembahasan

Contoh 1
Perhatikan gambar berikut!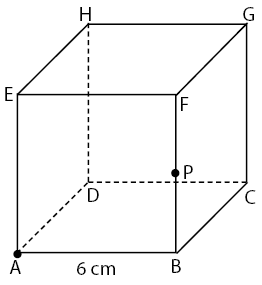
contoh soal mencari jarak titik ke titik pada dimensi tiga noh
Jika titik P berada pada tengah-tengah garis BF maka jarak antara titik A dan P adalah ….
A.    $5\sqrt{3}$
B.    $5\sqrt{2}$
C.    $3\sqrt{7}$
D.    $3\sqrt{5}$
E.    $3\sqrt{3}$ j

Pembahasan:

Perhatikan gambar di bawah!

jarak antara dua titik pada bangun ruang

Panjang $PB = \frac{1}{2} \cdot 6 = 3 cm$ dengan menggunakan rumus phytagoras, kita akan peroleh nilai AP seperti terlihar pada cara berikut.